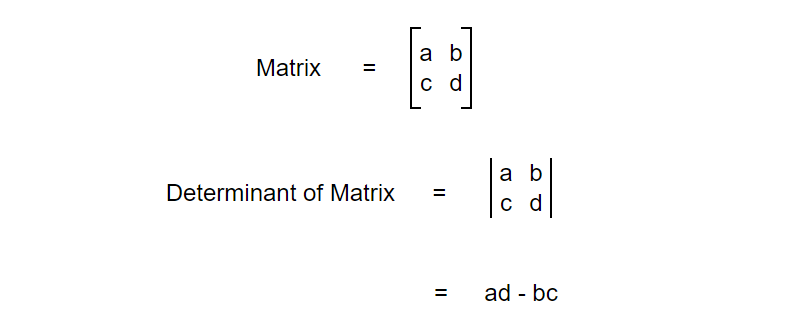
Eigenvalues and Eigenvectors

18-02-2023

Introduction to Vector, Basis & Span

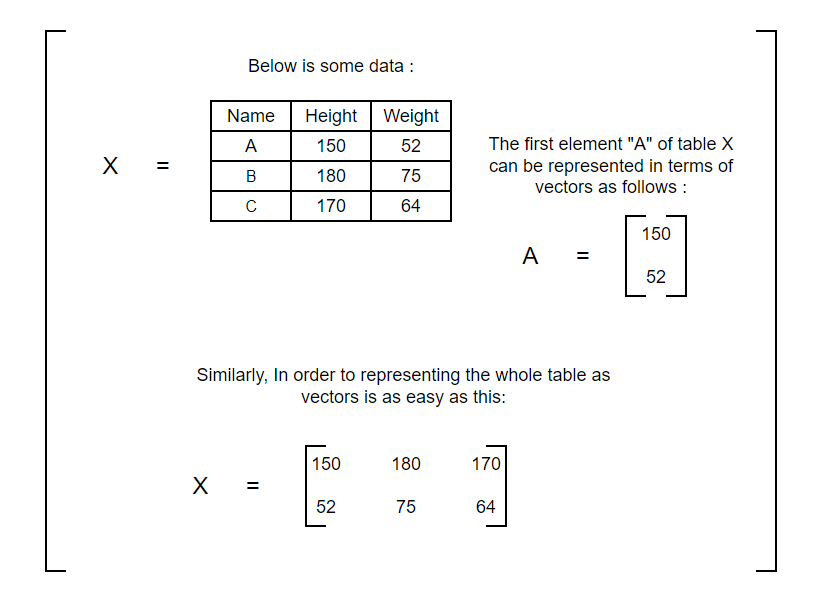
First concept we need to understand is vectors. Vectors are a simple way to represent data. How do they represent data? Let’s see with an example below:

Fig: Example -Vectors

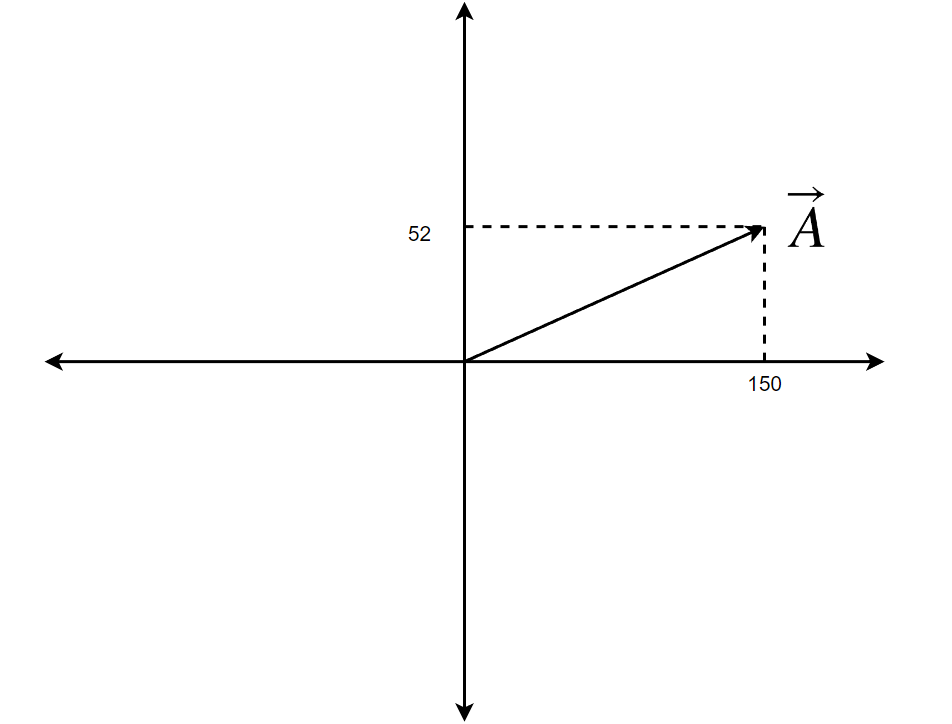
Now, Let’s look at how they are represented in coordinate axes.

Fig: Vectors in coordinate space

Looking at this, we can easily interpret what the vector A means. Generally, it's 150 units on the x-axis and 52 units on the y-axis.

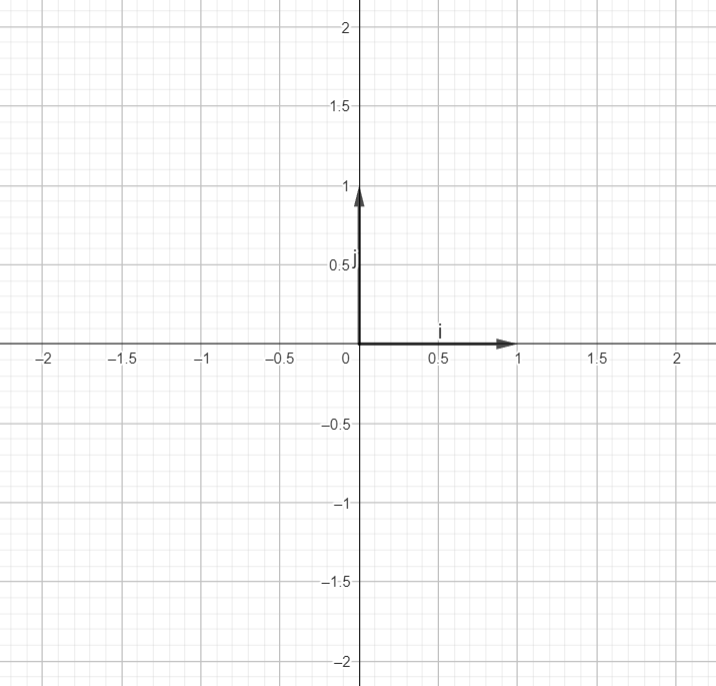
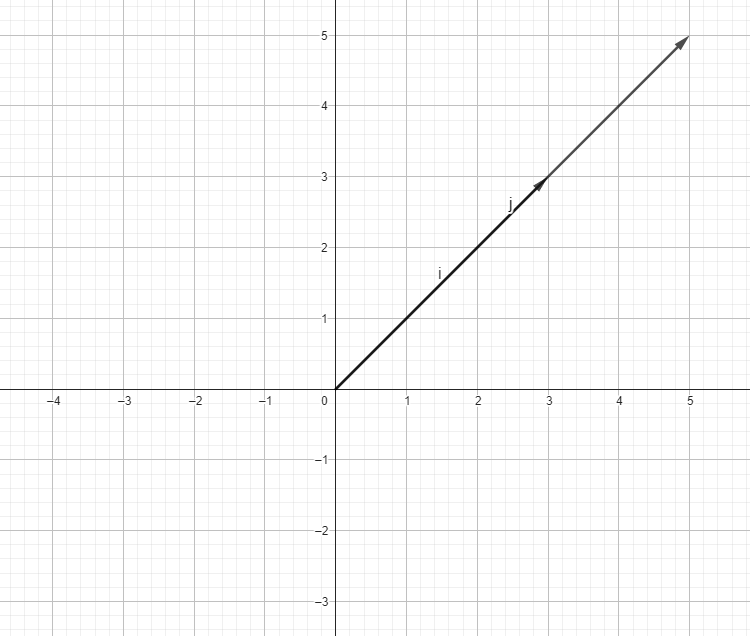
But we can try to look at it in a different manner. Let’s look at it in terms of basis vectors. So, basis vectors are the vectors that can be used in scaled combination with scalars in order to represent the entire coordinate axes. For xy coordinate space, we have î (called i hat) and ĵ (called j hat). î is the unit vector is x direction whereas ĵ is the unit vector in y direction. They are the standard basis vectors for the xy coordinate system.

Let’s look at how basis vectors are represented in coordinate axes.

Fig: Basis Vectors i & j

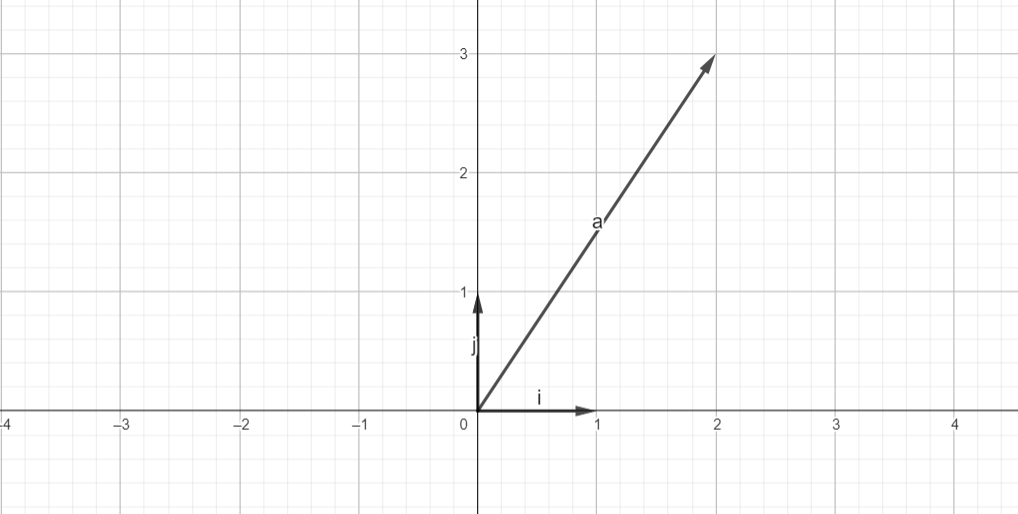
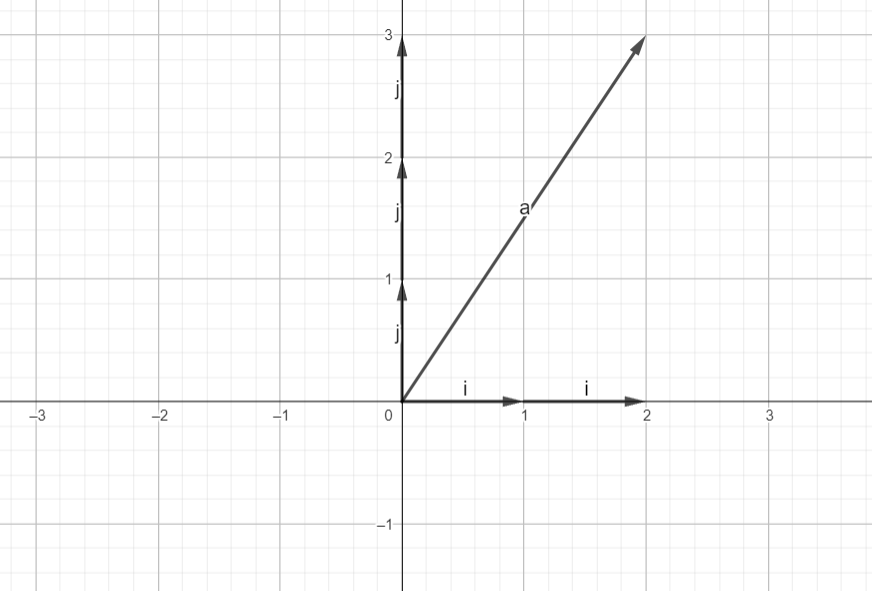
Now, Let’s consider a simple vector to understand it better.

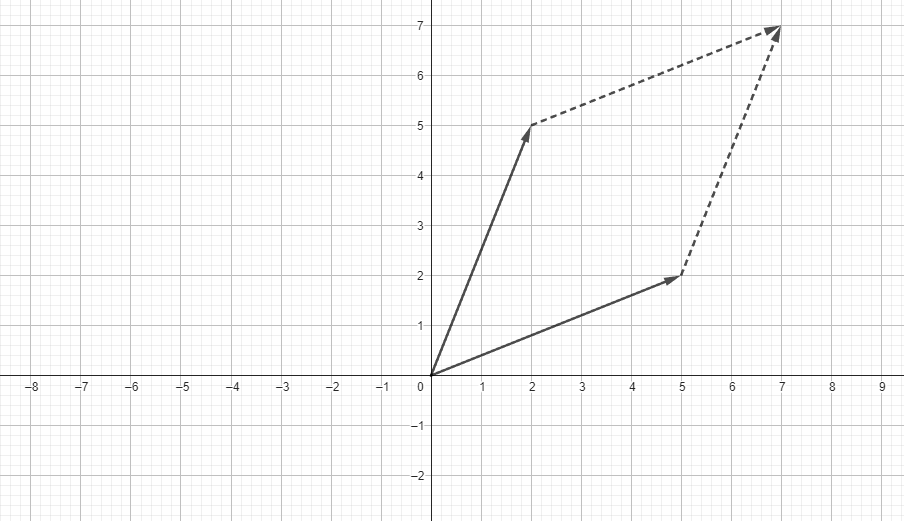
We can see that the vector at point (2, 3) can be represented using 2 basis components of x vector and 3 basis components of y vector.

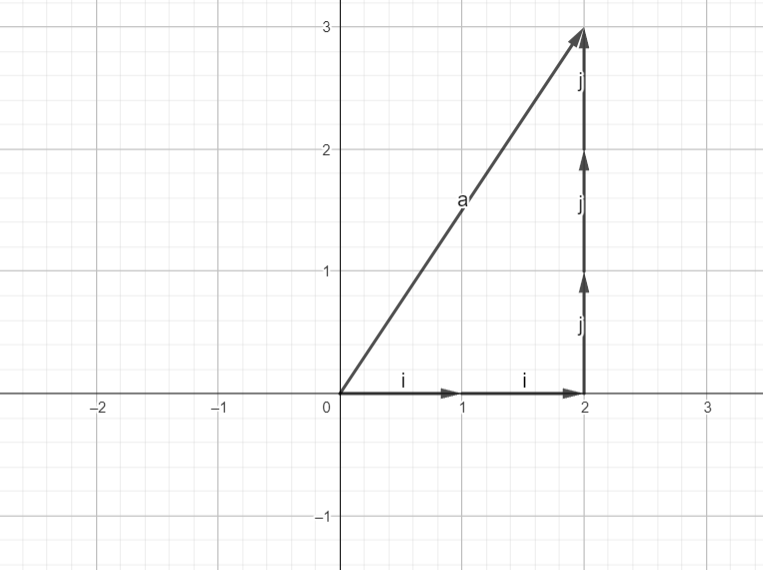
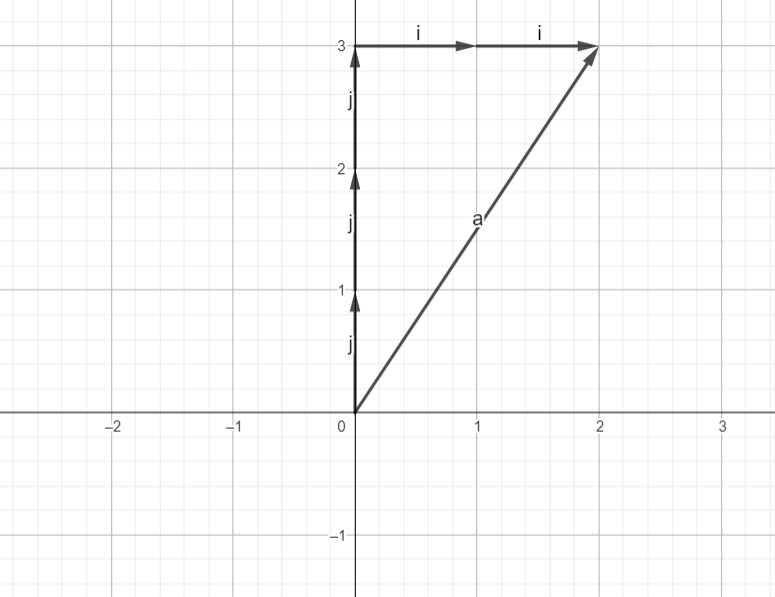
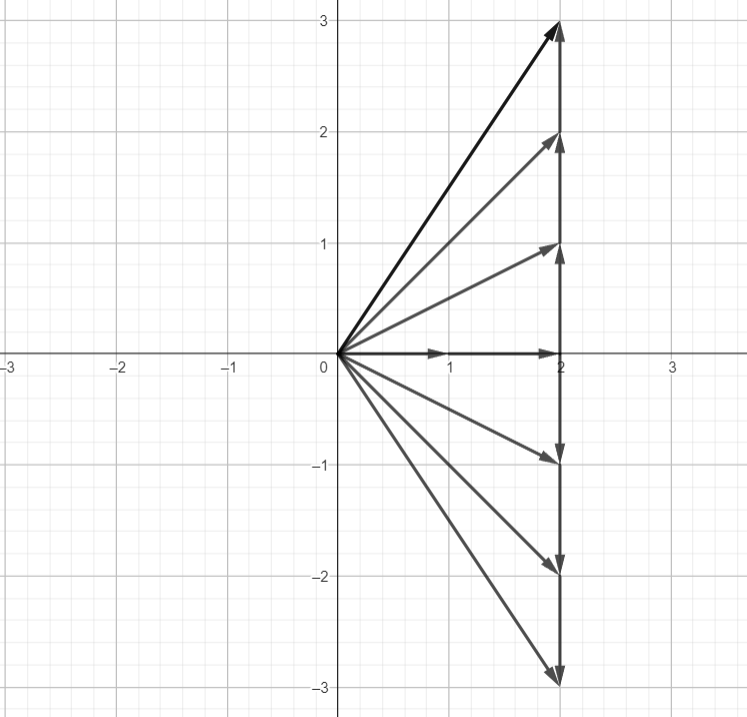
Now, we slide one of the basis components at the end of another to reach the point (2, 3).
We can move this way:

or we can move this way:

Both way we can reach the point (2, 3) with the help of basis vector.

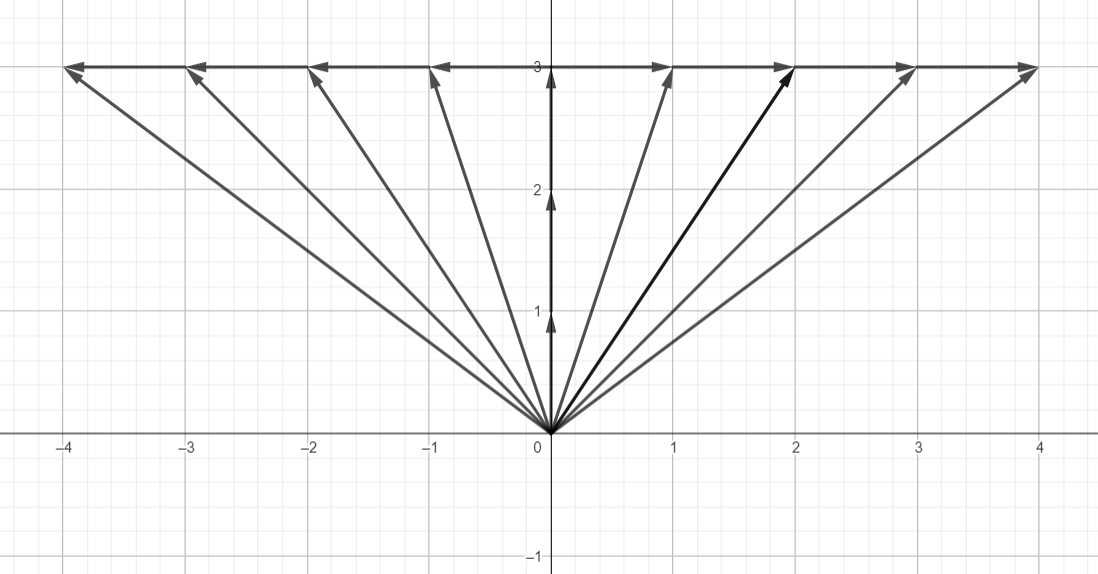
Observing the above example, it can be said that x-component of the vector is scaled extension of î and y_component of the vector is scaled component of ĵ. Thus, we can say that vector “a” is a scaled sum of two basis vectors. Also, We can represent any point in the coordinate axes using these scaled combinations. Fixing a basis vector and scaling another will give us a line as shown in the figure below.

Fig: Scaling î while keeping ĵ constant.

Fig : Scaling ĵ while keeping î constant.

This way of scaled combination is called Linear Combination. Actually, we could have used other vectors as our basis vector within the plane and the result would be the same i.e. can be scaled in combination to represent any points in the coordinate space. But for some basis vectors i.e. the ones lying in the same line, total representation space is just a line.

And the space that can be represented with the help of two basis vectors is known as span. So, for a basis vector to have a span of the entire coordinate space, they should be linearly independent.Below are some examples of basis vectors whose span is the entire coordinate space.

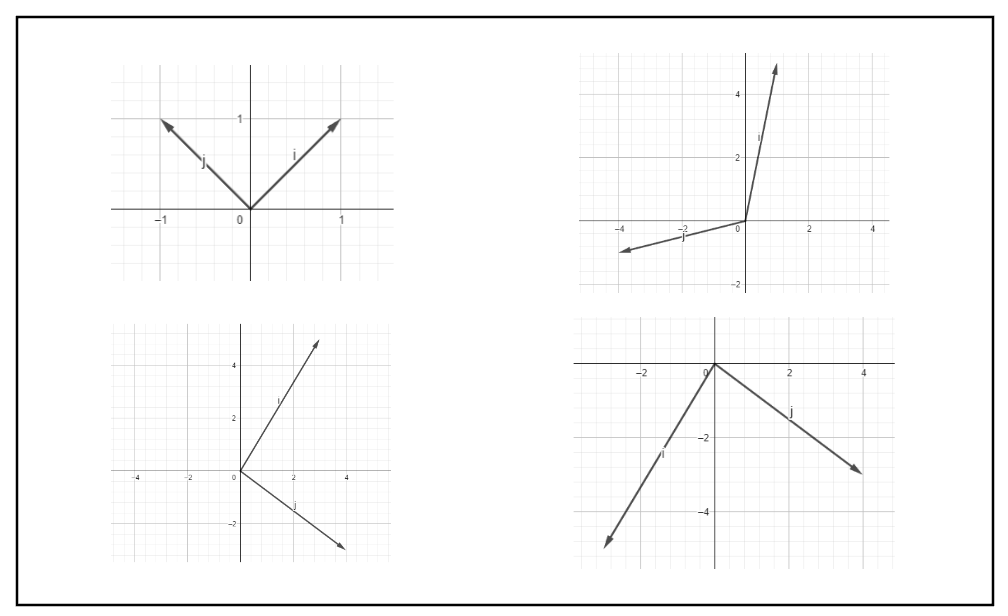
Below is a linearly dependent vector. It does not matter how much we try to scale it, it won’t represent anything other than a single line on which it lies.

Linear Transformation

Linear Transformation is a mapping between two vector spaces that respects vector addition and scalar multiplication. They are ways to move around space such that the grids between each unit remain parallel and evenly spaced among both axes.

Fig : Example - Linear Transformation

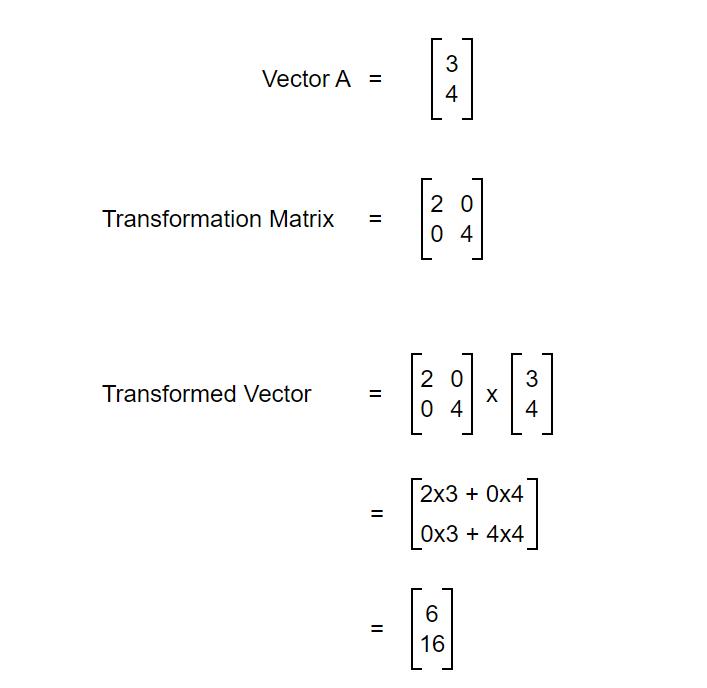
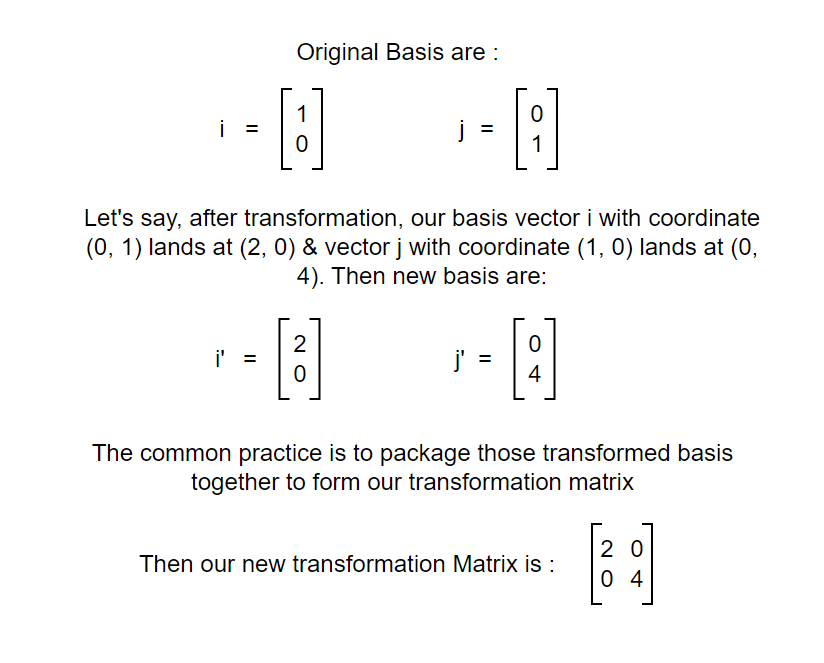
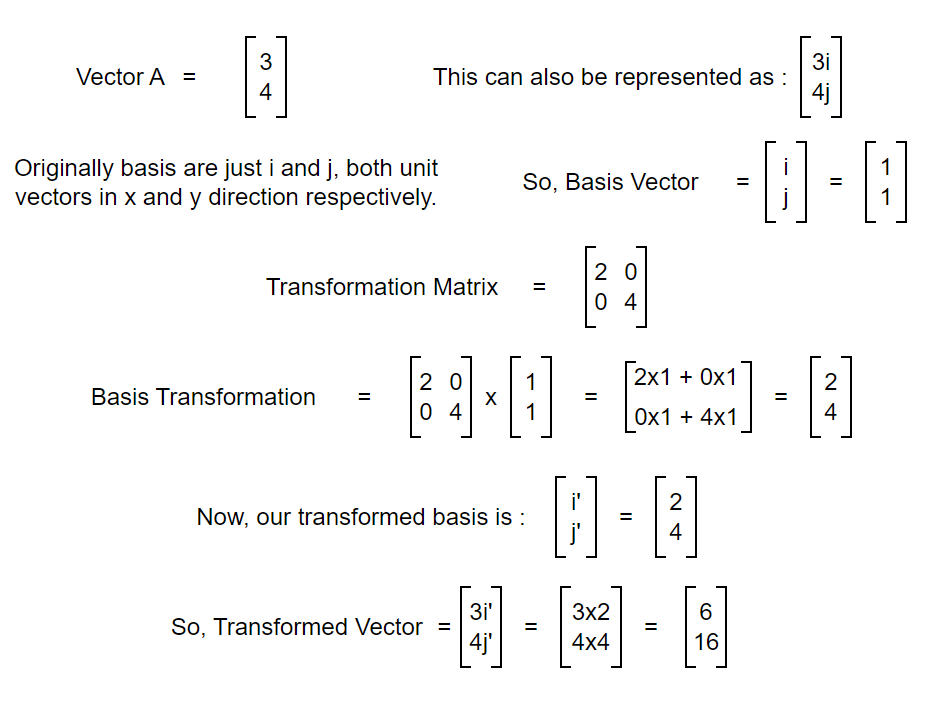
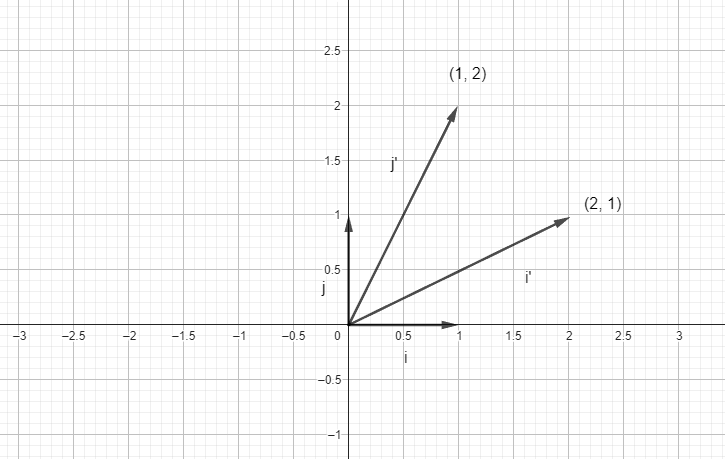
That is a straightforward thing where one vector is transformed into another. But what does it really mean?? Again, it can be viewed in terms of basis as shown in the figure below.

Fig : Linear Transformation in terms of basis vectors

So, matrix is just a way to package the basis transformation. Let’s say we have some transformation to do on a vector. We can transform the basis of that vector and calculate the transformation. Let’s see another example.

Fig : Example - Linear Transformation in terms of basis vectors

After transforming the basis, we are now able to transform the original vector. We now know about transformation and can transform vectors easily but what about the scale of transformation? By what factor was the area of the original vector increased or decreased? To understand this, let’s dive into the concept of determinants.

Determinants

Determinant inherently possess no meaning but it can have different meanings based on different conditions. Let’s start with a simple example:

Fig : Area covered by standard basis vectors

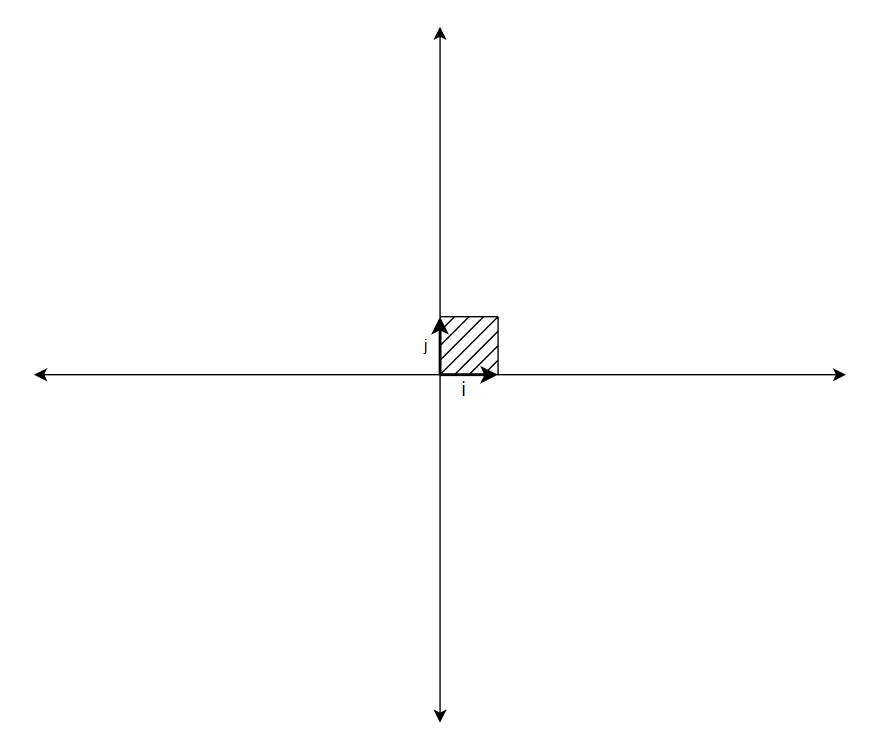
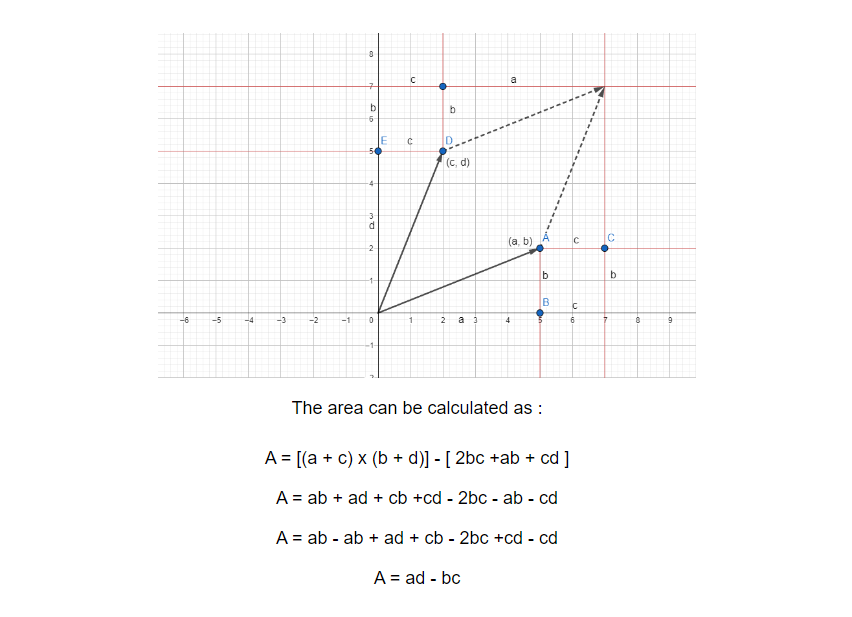
In the example above, we can see that the area covered by the basis vector is a unit square. Assume we have two vectors (a, b) and (c, d). First, let’s represent them in matrix form and calculate the determinant.

Fig : Calculating Determinant

We now slide both vector on top of each other and the area covered by them is as shown in the figure below:

To calculate the area covered by that region, we can simply do following:

Fig : Calculating Area covered by vectors

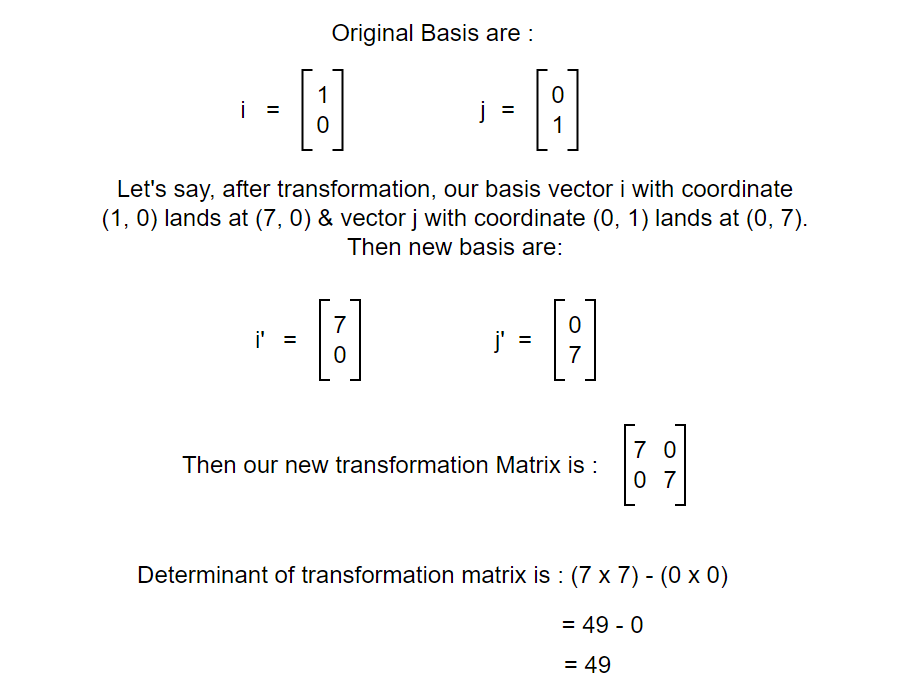
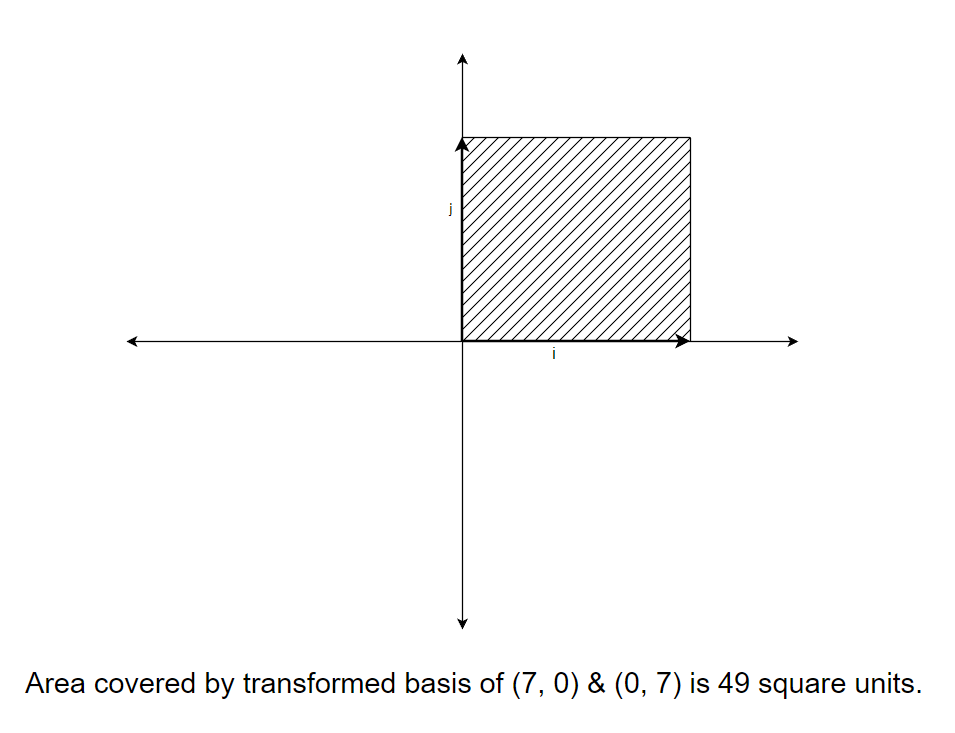
The area of the region turns out to be equal to the determinant. Now, let's look at it in terms of basis vectors.

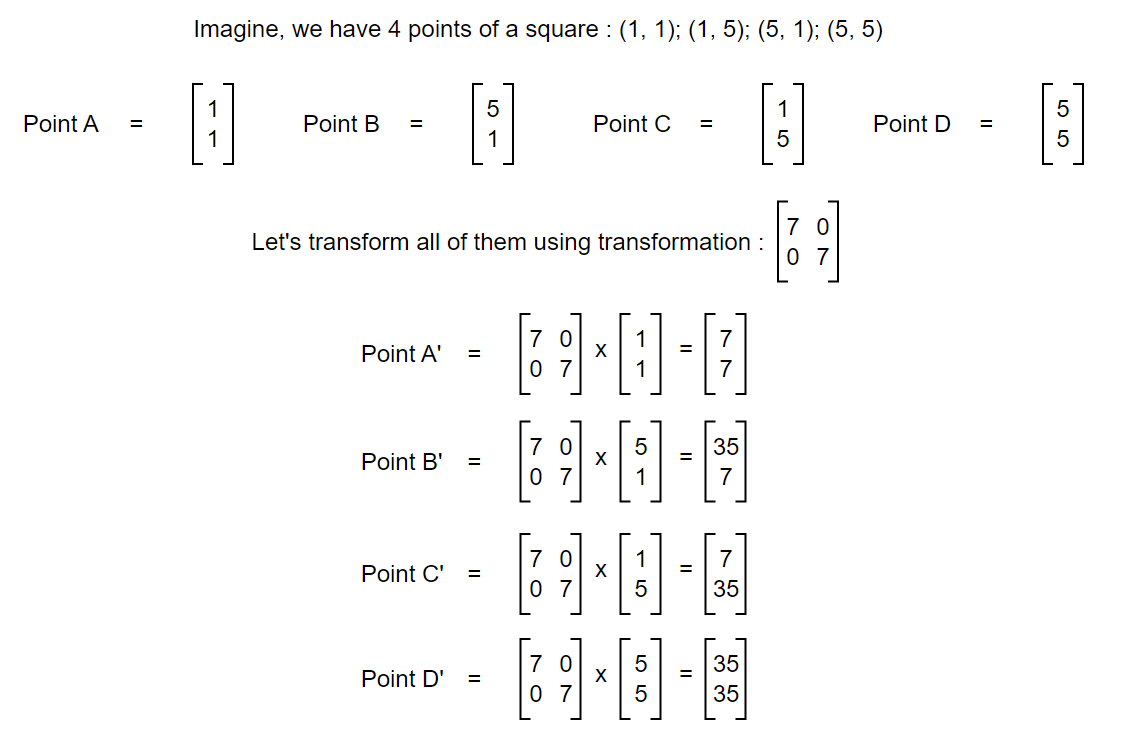
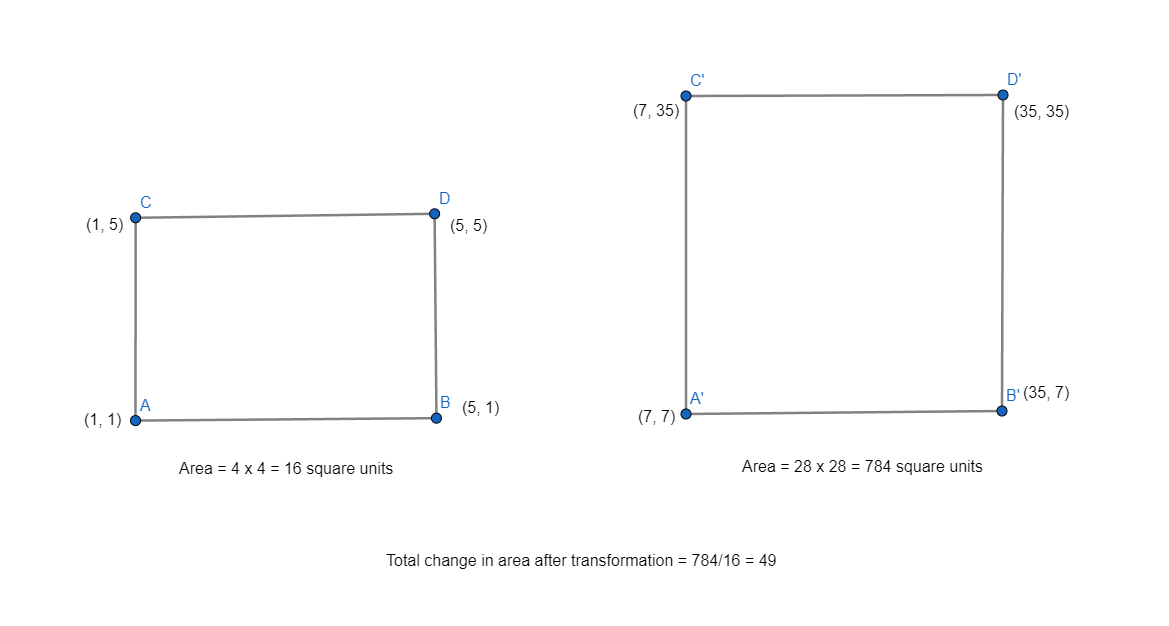
Let’s transform 4 different points that make a square and compare change in area.

In the examples above, we can see that the scale of transformation of the area enclosed by the original points to the area enclosed by transformed points is equal to the scale of transformation of the area enclosed by the original basis to the area enclosed by the transformed basis. And the determinant of the transformation matrix is the scale by which the original vector changes after transformation. So, Determinant can be looked as both area covered by the transformation matrix and the scale by which a transformation scales area enclosed by vectors. Now, let’s move in to concept of Eigenvalue and Eigenvectors.

Eigenvectors

In order to understand eigenvectors, consider a linear transform which moves î to (2, 1) and ĵ to (1, 2) and try out some examples.

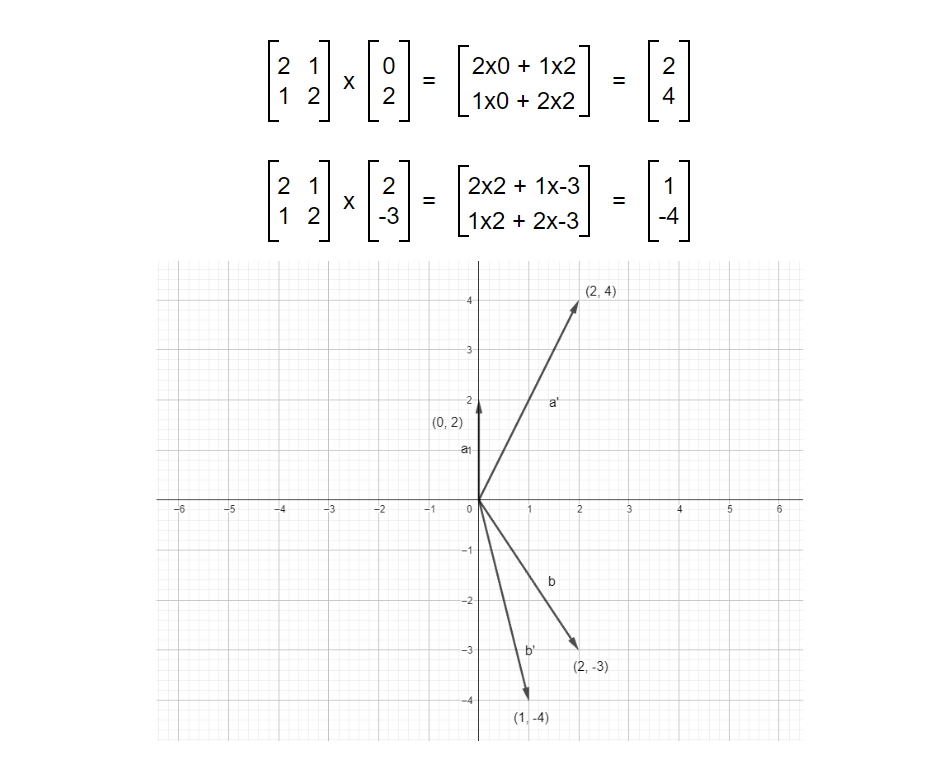
Transforming vector(0, 2) and vector (2, -3) with the transformation matrix.

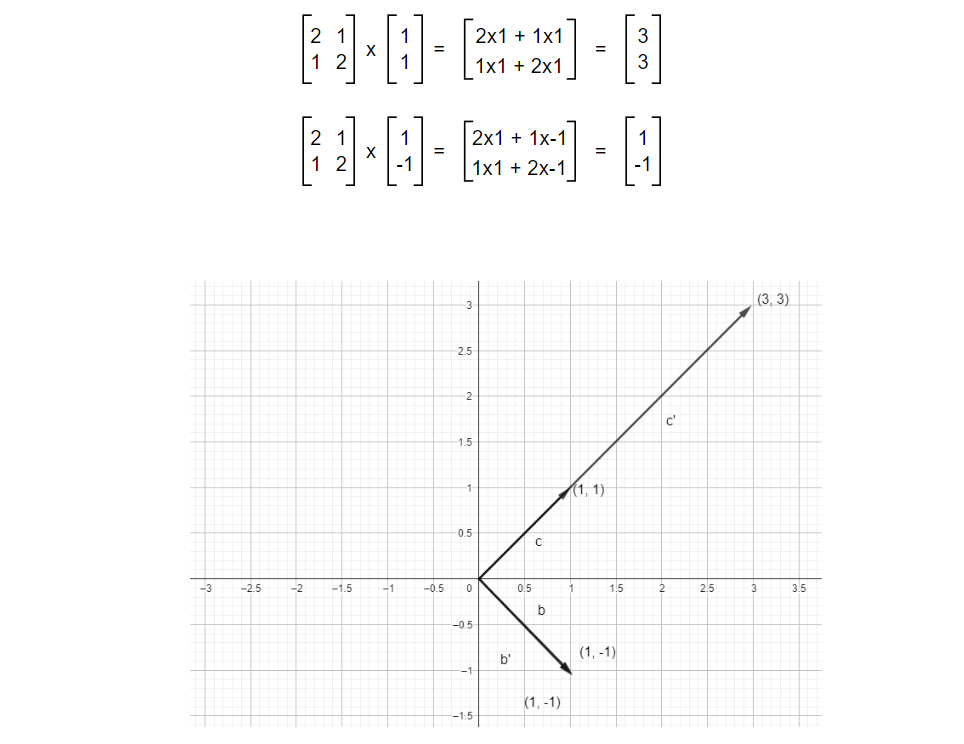
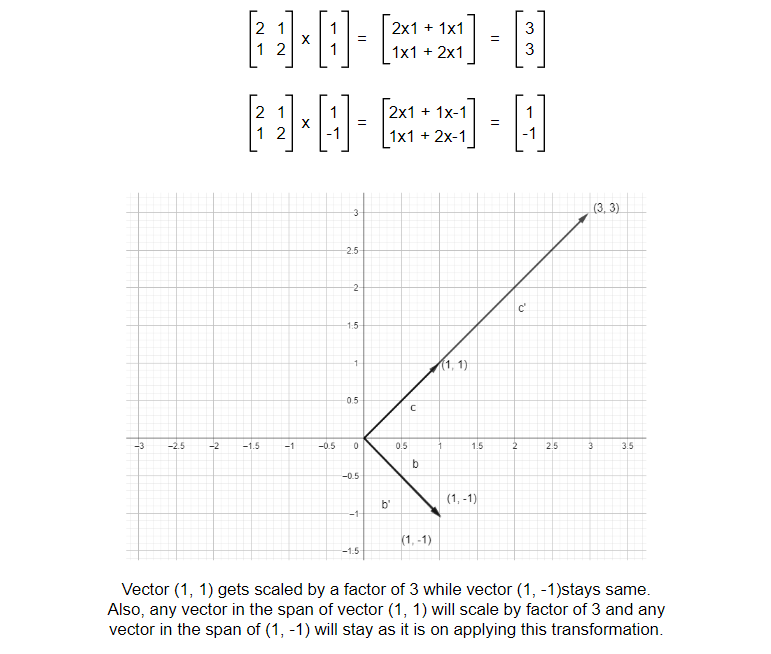
Just like the above examples, most vectors will change their position but some vectors will only stretch or diminish within their span (span of a single vector is a line). No matter what we do, the vector will stay in its position. Below is an example of such vectors.

We can see that one of the vectors got scaled while another stays the same. And these vectors are the Eigenvectors i.e. those vectors that do not shift or rotate but stay in it’s own span and scales by a factor on applying transformation are known as Eigenvectors of that transformation. Transformation was applied to the vector but the result of transformation turned out to be a scaled version of the original vector rather than rotated and scaled one.

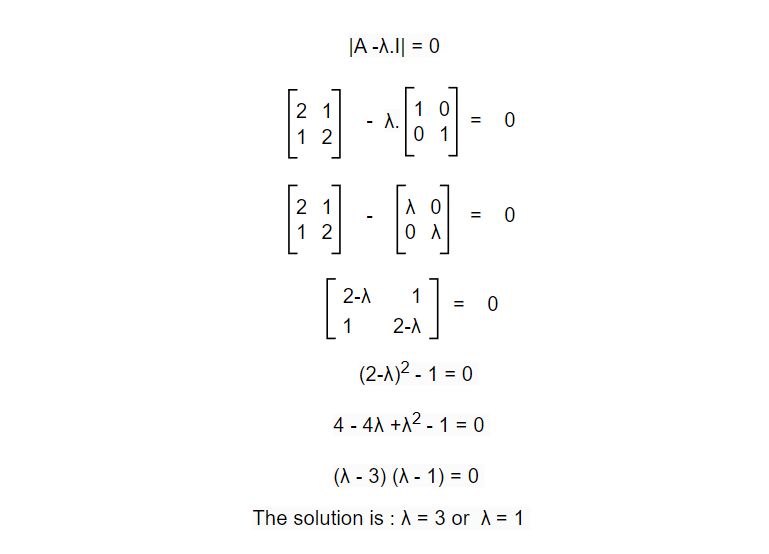
Now, calculate the eigenvalues for the transformation vector above.

But what does eigenvalues mean? We got λ = 3 or λ = 1. Let’s look back at one of the earlier examples. For this transformation matrix, eigenvectors are vectors at the span of (1, 1) and (1, -1). Meaning any vector in the span will not change its position after applying the transformation & the eigenvalue λ = 3 or λ = 1 means that one of the vectors will scale by a factor of 3 while other will remain as it is.

The practical applications of this concept are numerous. Particularly prominent within the field of Artificial Intelligence, eigenvalues find utility in various areas including Principal Component Analysis (PCA), regularization and weight initialization techniques, the realm of Graph Neural Networks, and even in enhancing our comprehension of overfitting, among a plethora of other applications. In conclusion, the significance of eigenvalues extends across diverse domains, with their pivotal role resonating notably in Artificial Intelligence, underpinning essential processes and fostering a deeper understanding of intricate phenomena like overfitting. Their versatile applications underscore their status as a fundamental concept with enduring impact.

References for this blog (Click on references for more info):

    1. Linear Algebra by 3Blue1Brown (Best resource ever).
    2. Eigenvalues and Eigenvectors of a Matrix.
    3. Eigenvector and Eigenvalue.
    4. Eigenvalues and Eigenvectors (MIT).
    5. Matrices by Eddie Woo.
    6. What is Determinant?.
    7. The deeper meaning of matrix transpose.
    8. What is a Determinant?.
    9. Dear linear algebra students, This is what matrices (and matrix manipulation) really look like.